https://zsr.github.io/2016/10/17/Google-S2/
Google S2作用:
根据多边形的边界区域映射成由许多一维数值构成的集合,这样就可以由这个集合代替多边形区域,便于后续计算。
典型的可以将不同国家(或者地区)的边界区域(经纬度)计算成一维数值的集合,可以用于判断该区域的任何一个坐标是否包涵在内,简单的说就是地理定位。
s2库提供了一个Cell的概念,每个Cell相当于一个单元格,在一个单元格内的所有Point,都可以算出同一个CellId。同时可以认为,一个Polygon可以用一个Cell的集合来表示。
那么这时的步骤就是通过区域的坐标,来初始化其内包含的所有的CellId,将这些CellId的id放入redis中做key,对应的value是区域名称(譬如,上海浦东新区),构建完全国范围的CellId后,查询用户的区域就可以通过用户的坐标获得一个CellId,然后去redis中查询,在使用LocalCache后,基本就没有什么计算成本,完全可以满足性能需求。
操作步骤:
1)首先获取地域图形的坐标点集合,可以从Natural Earth网站获取全球的坐标元数据(.shp文件)。
2)解析shp文件,生成区域坐标集合,这里选择pyshp(解析shp文件的python插件),这里需要注意:同一个国家可能包涵多个区域(muti Polygon),需要分开处理。下载地址:https://pypi.python.org/pypi/pyshp/
3)使用Google S2将多边形的边界坐标集合转化为一维数值集合,代表这个多边形的覆盖区域。
S2原理:
| 1234567891011 | S2RegionCoverer coverer = new S2RegionCoverer();ArrayList<S2CellId> covering = new ArrayList<S2CellId>();coverer.setMinLevel(minLevel);coverer.setMaxLevel(maxLevel);coverer.setMaxCells(1000000);S2Polygon s2Polygon = S2Polygon.makePolygon(polygonValue);//getCovering()表示可以最小程度覆盖整个区域,外接多边形coverer.getCovering(s2Polygon, covering);//getInteriorCovering()表示最大程度填充整个区域,内接多边形// coverer.getInteriorCovering(s2Polygon, covering);System.out.println(“covering of size:” + covering.size()); |
这里采用getCovering()外接多边形模式,避免多边形区域有盲点。MinLevel=9,MaxLevel=14
说明:MaxLevel最多可以设置30级,每升一级精度提升接近4倍,14级单个Cell可以表示范围:200平米~400平米,层级越高,构建越慢。
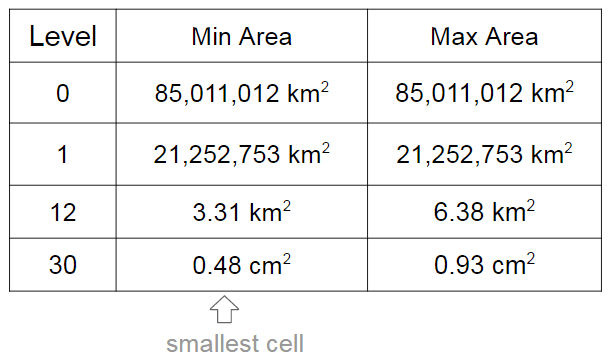
S2需要将地理位置表示为计算机可以理解的方式,即二进制码的表示,所以我们的目标就是用二进制码来表示三维空间。如何来做呢?需要进行降维。
1) 首先从三维降到二维,我们将地球放在一个正方体中,假设地球中心发光,光线穿过球体表面到达正方体平面的点就是球体表面的点的投影。于是我们就可以将地球投影到正方体的六个正方形表面。
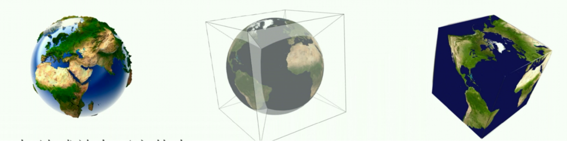
通过投影我们可以将三维球体映射到二维平面,但是这个方法有一个问题,就是投影长度的比例不同。水平方向上的投影长度比上下两端的投影长度小,这就造成了投射面积不均匀,会影响以后对地图的切分。解决方法就是再进行一次区间转换,对长度进行微挑,将长的拉短,短的拉长,尽量使投影面积分布均匀。
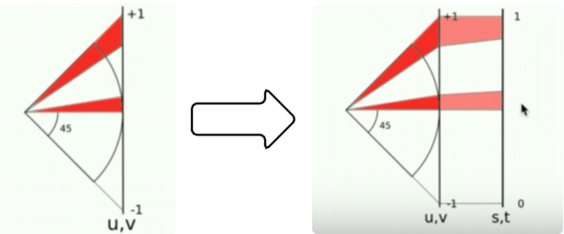
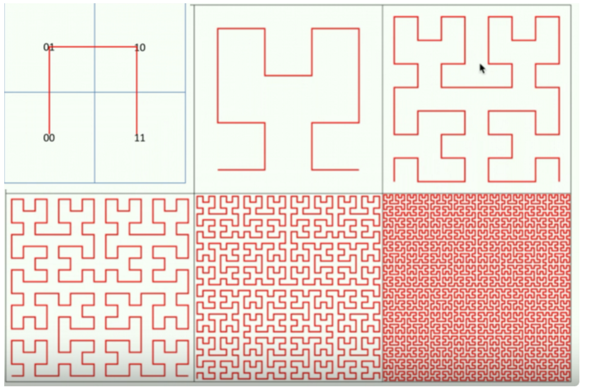
2) 将二维变成一维。我们有很多点组成的正方形平面,如何对这个平面进行一维表示呢?方法就是遍历,比如我们就可以用00 01 10 11来表示下面四个点组成的平面。将这种方法不断扩展到极限,我们可以得到填充整个二维平面的一条曲线,这就是著名的希尔伯特曲线(Hilbert Curve)。希尔伯特曲线可以把二维平面映射到一条线段上,它还有一个优势就是可以保存局部性,即空间位置相近的点在希尔伯特曲线上的位置也是相近的。
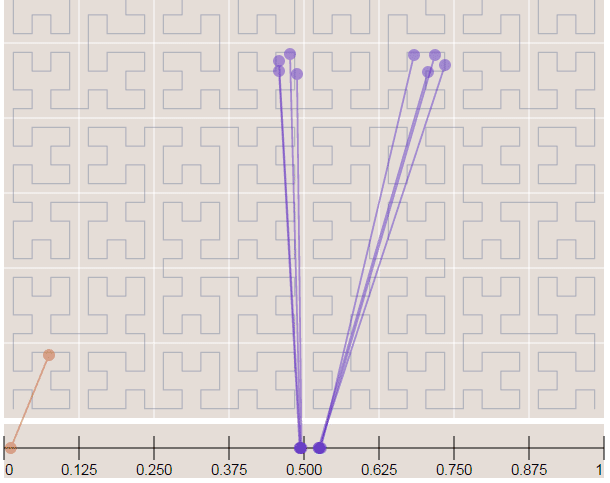
可以发现位置相近的二维坐标在一维线段上面也是邻近的。
3) 创建cell集合:
简单来说,就是将一个能完整覆盖多边形面积的cell,不断的划分(4块cell),如果4快仍然全部与多边形相交则继续划分,否则有一个或多个cell不与多边形相交则抛弃,直至最大划分到maxLevel。可以发现如果maxLevel设置的越大,则精度越高(测试效率来看,maxLevel设置为14,15级已经比较精确,层级大于15级非常影响生成cell的效率)。
这里假设多边形区域为二维图形,如果需要对该图形进行覆盖,可能有以下可能:
- cell被包含在多边形内部
- cell与多边形相交(有一部分在外面)图中大的cell和多边形相交,如果该cell的level已经达到maxLevel则停止划分,并将这个cell加入最后集合;如果这时候该cell的level小于maxLevel,则继续划分为4小块(不一定等分),可以发现有2个小的cell仍然与多边形相交,如果这2个cell层级已经达到MaxLevel则将这2个加入最终集合,否则继续划分,另外2个cell已经在多边形的外面则抛弃,
如果多边形内部可以完整填充一个cell(注意限制:minLevel,maxLevel; 级别越小,cell越大),则将该cell直接添加到集合中。比如这里设置的minLevel=9(一般只有面积非常大的国家才会有level=9),所以多边形区域所能生成的最大面积cell只有可能是level=9.
根据实际测试来看,像美国,俄罗斯相对面积比较大的国家,最小的level可以达到7(目测地球所有国家中最小的level就是7),也就是说这些国家的面积可以内涵完整的level=7的cell,这么做可以将许多高层次的cell由一个低层次的cell替代,减少了生成的cell数量同时表示的范围没有变化。
之所以这里选择minLevel=9,是为了以后定位方便,目前的定位是通过经纬度由Google S2生成CellId,再由这个CellId查询所有的CellId集合,如果有匹配的则命中。匹配的代码 如下:
| 123456789 | int minLevel = 9;int maxLevel = 14;for (int i = minLevel; i < (maxLevel + 1); i++) { paCell = s2cell.parent(i); if (cellIds.contains(paCell.id())) { System.out.println(“命中!!!”); break; }} |
匹配的规则:先从最低级别判断,如果没有被包含在CellId集合中则判断其父层是否被包含,这样逐层递增直至maxLevel。所以minLevel设置的太小会增加判断次数,在并发比较大的情况下会影响效率。
